CGLS 3D (ToMoBAR)#
Description
Conjugate Gradient for Least Squares (CGLS) is an iterative approach to solve the reconstruction problems via least-squares minimisation. The algorithm aims to solve the system of normal equations \(\mathbf{A}^{\intercal}\mathbf{A}x = \mathbf{A}^{\intercal} b\), where \(\mathbf{A}\) is the forward projection or geometry matrix, \(x\) is the sought solution (reconstructed image), \(b\) is the vectorised projection data, and \(\mathbf{A}^{\intercal}\) is the inverse projection operator.
Where and how to use it:
When the tomographic data is noisy, incomplete, or/and it is the limited-angle data. CGLS is more efficient and accurate than classical iterative methods but requires careful handling of the number of iterations to avoid amplifying noise (method’s divergence). Normally, noise amplification or overfitting can happen when too many iterations performed.
What are the adjustable parameters:
The number of
iterationsis an important parameter as too few iterations leave the reconstruction blurry, while too many lead to noise amplification. Keep the total number of iterations within the 15-30 range is usually a good practice.
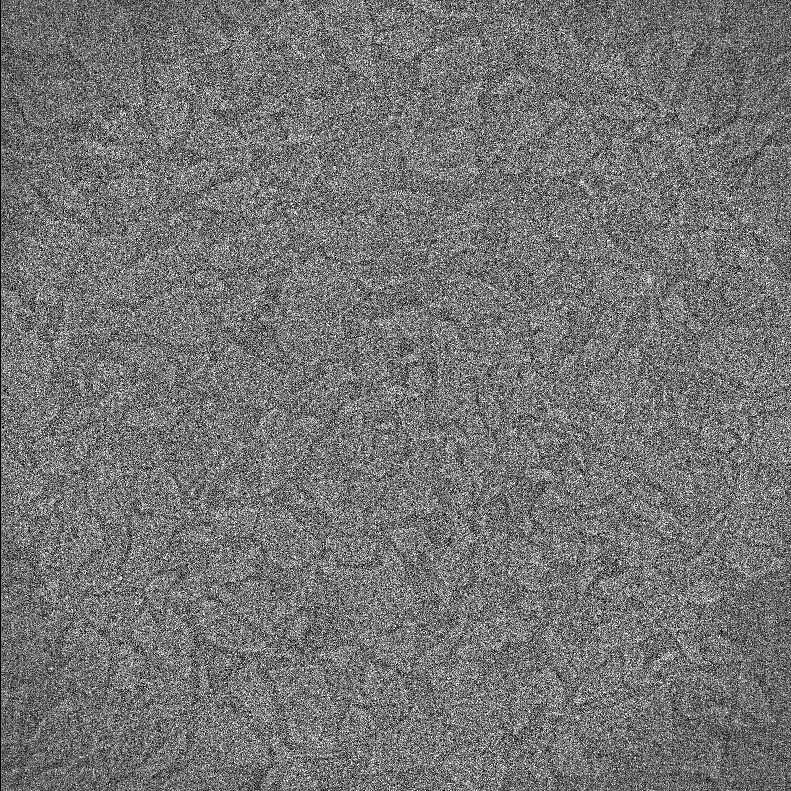
Fig. 57 Log-Polar 3D (ToMoBAR) reconstruction is extremely noisy as the data is undersampled with a rapid exposure to the X-ray beam.# |

Fig. 58 CGLS reconstruction with |
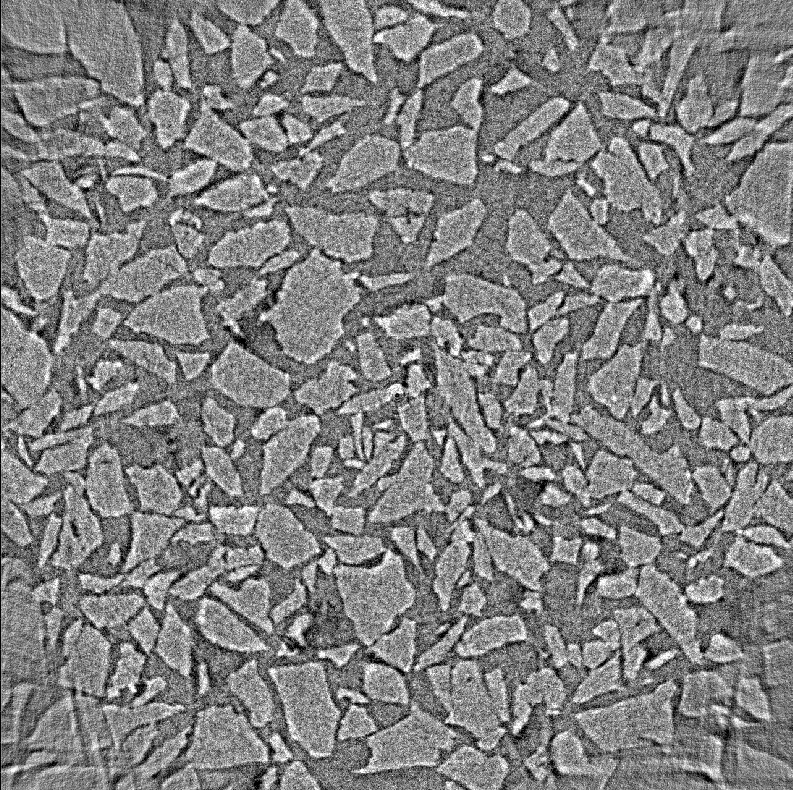
Fig. 59 CGLS reconstruction with |
nonnegativity. By setting this parameter toTrueimposes positivity constraint on the solution. In some cases that can improve the contrast.
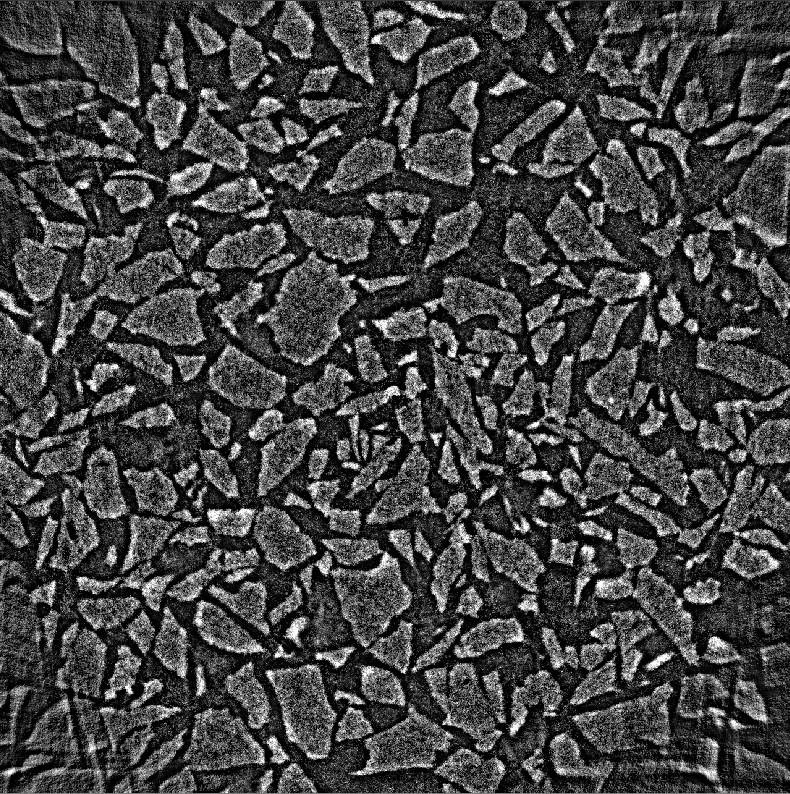
Fig. 60 CGLS reconstruction with iterations=15 and nonnegativity=True.#